Maths week 11 graded assignment Complete Solutions Are Discussed In This Blog We Hope This Might Help You All In Matching Answers . Or For Some Others Reasons Not Able To Complete Graded Assignments
USE THE FOLLOWING INFORMATION FOR QUESTIONS [7-8]:
Shreya needs to perform 10 tasks namely {�,�,�,�,…..�A,B,C,D,…..J}. Some tasks needs to be performed after performing a particular task. In the below table, column 1 shows the tasks and column 2 shows the sets of tasks that can be performed only after performing the particular task.

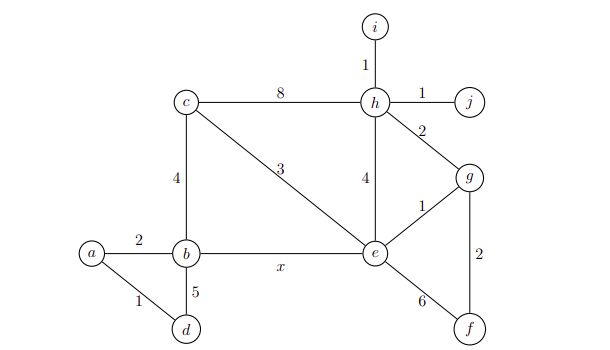
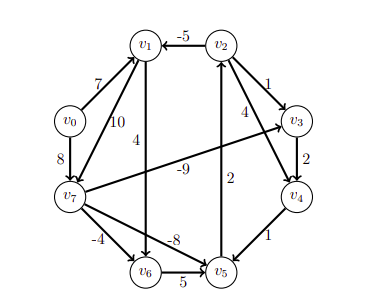
(Use the following information for questions 10 & 11)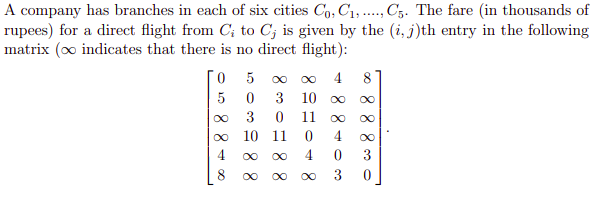
(Use the following information for questions 12 & 13)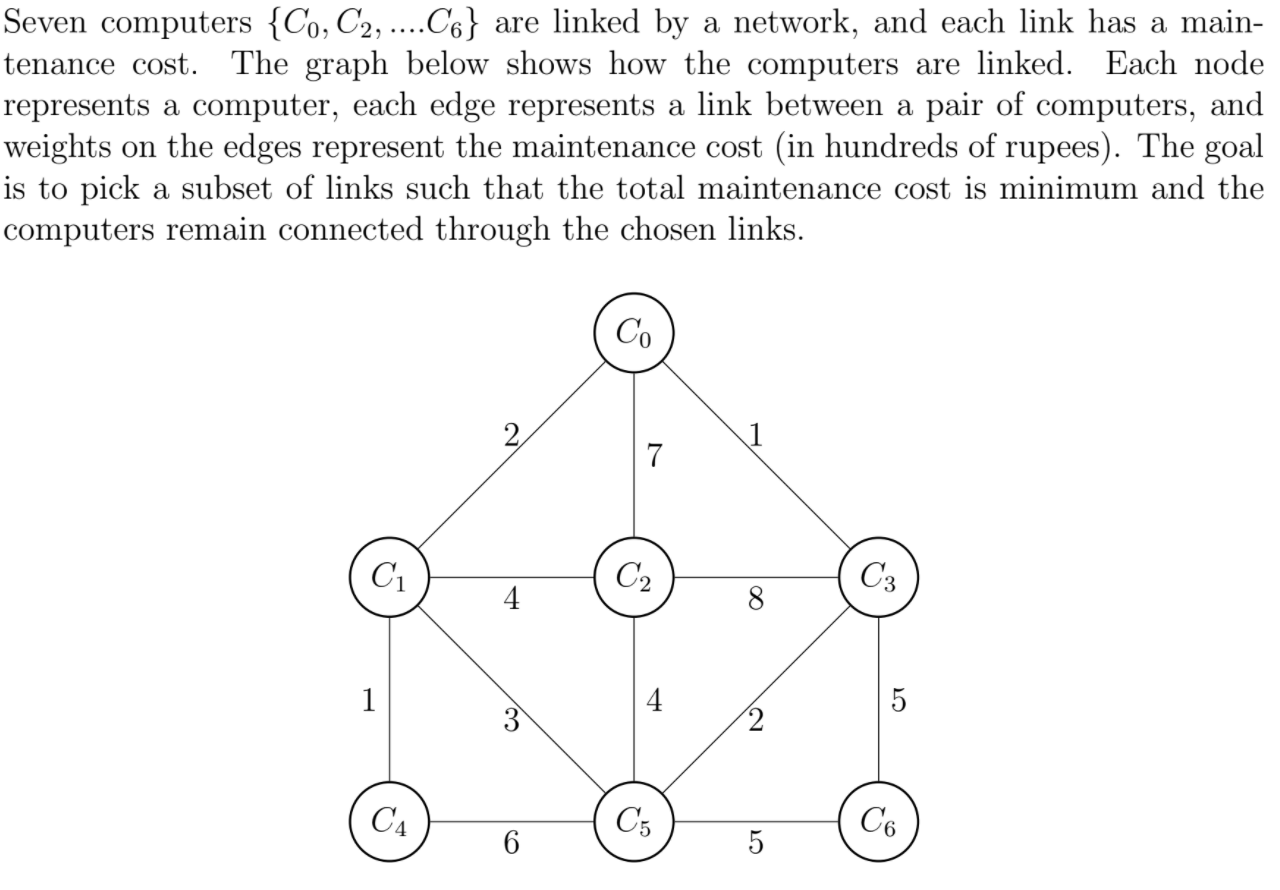
(Use the following information for questions 14 & 15)

I can’t see Correct answer.
Can you provide one shot Hindi based lecture of IIT M week basis?
(YouTube channel)
Very Soon Already Team Is Working On It