Computational Thinking week 11 graded assignment Complete Questions Are Discussed In This Blog. Access From Below Link
1.reverse is a recursive procedure to reverse a list. Select the correct code fragment to complete the pseudocode given below. It is a Multiple Select Question (MSQ).
1Procedure reverse(L)2 if(length(L) <= 1){3 return(L)4 }5 *********************6 * Fill the code *7 *********************8End reverse9
return([last(L)] ++ reverse(init(L)))
return([first(L)] ++ reverse(rest(L)))
return([last(L)] ++ reverse(init(rest(L))) ++ [first(L)])
return([first(L)] ++ reverse(init(rest(L))) ++ [last(L)])
return([last(L)] ++ reverse(rest(init(L))) ++ [first(L)])
Question:2-4:
An auto-grading system for an online course is designed in the following way:
∘∘ The “roll” key maps to the student’s roll number.
∘∘ The “time” key maps to the time of submission
∘∘ The “score” key maps to the student’s score for that submission
∙ ∙ Each student can make multiple submissions before the deadline.
∙ ∙ Every time a student makes a submission, the dictionary corresponding to it is appended to the end of a list called scores.
An example:
scores = [{“roll”: 12, “time”: 10:20, “score”: 80 },
{“roll”: 20, “time”: 11:23, “score”: 70 },
{“roll”: 12, “time”: 20:40, “score”: 90 },
{“roll”: 12, “time”: 23:50, “score”: 95 },
{“roll”: 20, “time”: 23:53, “score”: 65 }]
Study the following pseudocode:
Procedure isPresent(L, roll)
foreach D in L{
if(D[“roll”] == roll){
return(True)
}
}
return(False)
End isPresent
Procedure getSubs(L)
firstSub = {}, restSub = []
if(length(L) <= 1){
return(L)
}
firstSub = first(L)
restSub = rest(L)
if(isPresent(restSub, firstSub[“roll”])){
return(getSubs(restSub))
}
else {
return([firstSub] ++ getSubs(restSub))
}
End getSubs
submisssions = []
scores = [ {“roll”: 12, “time”: 10:20, “score”: 80 },
{“roll”: 20, “time”: 11:23, “score”: 70 },
{“roll”: 12, “time”: 20:40, “score”: 90 },
{“roll”: 12, “time”: 23:50, “score”: 95 },
{“roll”: 20, “time”: 23:53, “score”: 65 } ]
submisssions = getSubs(scores)
2. What is the value of submissions?
[ {“roll”: 12, “time”: 10:20, “score”: 80 },
{“roll”: 20, “time”: 11:23, “score”: 70 } ]
[ {“roll”: 20, “time”: 11:23, “score”: 70 },
{“roll”: 12, “time”: 10:20, “score”: 80 } ]
[ {“roll”: 12, “time”: 23:50, “score”: 95 },
{“roll”: 20, “time”: 23:53, “score”: 65 } ]
[ {“roll”: 20, “time”: 23:53, “score”: 65 },
{“roll”: 12, “time”: 23:50, “score”: 95 } ]
3.What does the variable submissions represent?
The list of all the submissions made by the students sorted in the ascending order of time.
The list of all the submissions made by the students sorted in the descending order of time.
The list of the last submissions made by the students sorted in the ascending order of time.
The list of the last submissions made by the students sorted in the descending order of time.
The list of the first submissions made by the students sorted in the ascending order of time.
The list of the first submissions made by the students sorted in the descending order of time.
4.Assume that reverse is a procedure that reverses a list. Which of the following statements returns the list of the first submissions made by the students sorted in the ascending order of time?
getSubs(scores)
reverse(getSubs(scores))
getSubs(reverse(scores)))
reverse(getSubs(reverse(scores)))
5.outcomes is a list of strings that contains the information about the outcome of cricket matches played by India in a tournament. Assume that each element in the list is either “win” or “loss”. For example, if five matches have been played, then outcomes could look like this:
[“won”, “lost”, “lost”, “won”, “won”]
We call a list of outcomes a blank slate if the number of wins is equal to the number of losses. blankSlate is a procedure that accepts outcomes as input and returns True if it is a blank slate and False otherwise. Select the correct code fragment to complete the following pseudocode. It is a Multiple Select Question (MSQ).
1Procedure blankSlate(outcomes)2 if(numeric(outcomes) == 0){3 return(True)4 }5 else{6 return(False)7 }8End blankSlate9 10*********************11* Fill the code *12*********************
Procedure numeric(L)
if(length(L) == 0){
return(0)
}
if(last(L) == “won”){
return(numeric(init(L)) + 1)
}
else{
return(numeric(init(L)) − 1)
}
End numeric
Procedure numeric(L)
if(length(L) == 0){
return (0)
}
if(last(L) == “won”){
return(numeric(rest(L)) + 1)
}
else{
return(numeric(rest(L)) − 1)
}
End numeric
Procedure numeric(L)
if(length(L) == 0){
return(0)
}
if(first(L) == “won”){
return(numeric(rest(L)) + 1)
}
else{
return(numeric(rest(L)) − 1)
}
End numeric
Procedure numeric(L)
if(length(L) == 0){
return(0)
}
if(first(L) == “won”){
return(numeric(init(L)) + 1)
}
else{
return(numeric(init(L)) − 1)
}
End numeric
QUESTION-6-7
2n chess players are participating in a tournament. Each player is given a unique participant ID that is represented as a string. The player IDs are stored in a non-empty list players in the descending order of their rating, i.e., the first element in the list has the ID of the player with the highest rating.
The matches are scheduled as follows: The ��ℎith match is between the ��ℎith player from the top and the ��ℎith player from the bottom of the rating list. We wish to create a list called matches which stores the sequences of matches, starting with the first match and ending with the last match. Each match is represented as a list of two players, the first element of which is the ID of the player with the higher rating, while the second element is the ID of the player with lower rating. Assume that no two players have the same rating.
Answer questions 6 and 7 based on this information.
matchThem is a recursive procedure that accepts players as argument and returns matches. Select the correct implementation of the procedure. It is a Multiple Select Question (MSQ).
Procedure matchThem(players)
firstLast = [], middle = []
if(length(players) == 2){
return([players])
}
else{
firstLast = [first(players), last(players)]
middle = init(rest(players))
return([firstLast] ++ matchThem(middle))
}
End matchThem
Procedure matchThem(players)
firstLast = [], middle = []
if(length(players) == 2){
return(players)
}
else{
firstLast = [first(players), last(players)]
middle = init(rest(players))
return([firstLast] ++ matchThem(middle))
}
End matchThem
Procedure matchThem(players)
firstLast = [], middle = []
if(length(players) == 0){
return([])
}
else{
firstLast = [first(players), last(players)]
middle = init(rest(players))
return([firstLast] ++ matchThem(middle))
}
End matchThem
Procedure matchThem(players)
firstLast = [], middle = []
if(length(players) == 0){
return([players])
}
else{
firstLast = [first(players), last(players)]
middle = init(rest(players))
return([firstLast] ++ matchThem(middle))
}
End matchThem
7.matchThem is a non-recursive procedure that accepts players as argument and returns matches. Select the correct implementation of the procedure.
Procedure matchThem(players)
matches = [ ]
while(length(players) > 0){
matches = matches ++ [[last(players), first(players)]]
players = rest(init(players))
}
return(matches)
End matchThem
Procedure matchThem(players)
matches = [ ]
while(length(players) > 0){
matches = matches ++ [[first(players), last(players)]]
players = rest(init(players))
}
return(matches)
End matchThem
Procedure matchThem(players)
matches = [ ]
while(length(players) >= 0){
matches = matches ++ [[first(players), last(players)]]
players = rest(init(players))
}
return(matches)
End matchThem
Procedure matchThem(players)
matches = [ ]
while(length(players) > 0){
matches = matches ++ [[first(players), last(players)]]
players = rest(players)
}
return(matches)
End matchThem
Question 8-11
Consider the following graph with six nodes. A is a 6 × 6 matrix corresponding to this graph. Assume that it has already been computed:
In the following pseudocode:
- graph is a matrix
- parents is a dictionary
- sequence is a list
Procedure DFS(graph, parents, sequence, i)
sequence = sequence ++ [i]
foreach j in columns(graph){
if(graph[i][j] == 1 and not(isKey(parents, j))){
parents[j] = i
parents, sequence = DFS(graph, parents, sequence, j)
}
}
return(parents, sequence)
End DFS
Answer questions 8 to 11 using the information given above. In all questions, S represents a list, P represents a dictionary, while A and B represent matrices.
8.What will be the value of S after executing the following pseudocode?
1P = { }2S = [ ]3P[0] = -14P, S = DFS(A, P, S, 0)
[0, 1, 2, 5, 3, 4]
[0, 1, 4]
[0, 1, 2, 3, 5, 4]
[0, 3, 1, 4, 5]
9.What will be the value of nodes after executing the following pseudocode?
1P = { }2S = [ ], nodes = []3P[5] = -14P, S = DFS(A, P, S, 5)5nodes = keys(P)
[5, 2, 1, 0, 3, 4]
[5, 2, 1, 4, 0, 3]
[5, 2, 3, 0, 1, 4]
Cannot be determined
10.Assume that sort is a procedure that accepts a list of integers as input and returns a sorted list in ascending order. If 0 ≤ start ≤ 5, which of the following statements are true at the end of execution of the following pseudocode? It is a Multiple Select Question (MSQ).
1P = { }2S = [], nodes = []3P[start] = -14P, S = DFS(A, P, S, start)5nodes = sort(keys(P))
nodes is equal to [0, 1, 2, 3, 4, 5]
S is equal to [0, 1, 2, 3, 4, 5]
The value of nodes is independent of start
The value of S is independent of start
The graph is connected.
The graph is not connected.
11.Execute the following pseudocode
1P = { }2S = [ ]3P[3] = -1, parent = 04P, S = DFS(A, P, S, 3)5B = createMatrix(6, 6)6foreach i in keys(P){7 if(i != 3){8 parent = P[i]9 B[parent][i] = 110 }11}
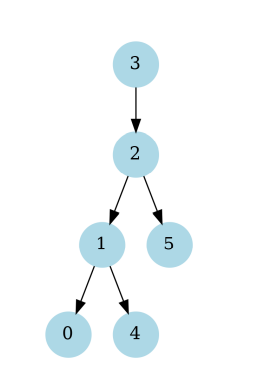
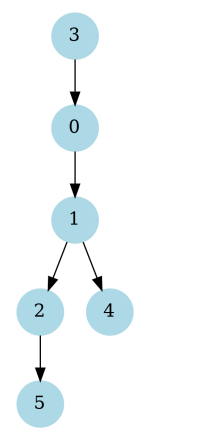 Correct Answer
Correct Answer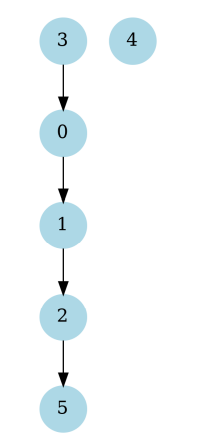
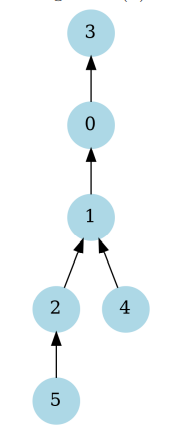

Thanks for your efforts 👍